Beware mean substitution ! (And the importance of mothers)

Today was a lesson in why one should always be a little leery of mean substitution. I had downloaded a data set to use as a logistic regression example for my class tomorrow. It happened to be the 2010 Monitoring the Future study and I was particularly interested in school drop out.

This is a sample of around 15,000 students in their senior year of high school. You would think that once students had made it to their senior year they would stick around and graduate. There were 90 students who said they didn’t expect to graduate, and about 14,000 who expected to graduate on time. (The rest either expected to graduate in the summer or did not answer.)

Because this was a student assignment, I didn’t want to bother with a huge data set. I used PROC SURVEYSELECT to pull a random sample of 500 students from those who expected to graduate and combined that with the 90 who didn’t for a comfortable sample size of 590.

One of the variables I wanted to use in my equation was Mother’s Education. This was on a scale from 1 (= grade school) to  6 (=graduate school).  There is a category 7= don’t know.

There were only 4% of the subjects who had put “Don’t know” for mother’s education and you might think it wouldn’t be a big deal to just use the mean. As an alternative, there are multiple imputation procedures for handling missing data. I could have gone with either of those alternatives and moved on. Instead, though, I got to thinking …

These aren’t little kids in elementary school. These are high school seniors. Why DON’T they know how much education their mother has?

My husband died when my children were 8, 9 and 12 years old. I had a good friend whose wife died when his children were almost the exact same ages. On more than one occasion when we’ve been discussing how life turned out, he’s said to me very seriously,

I think my kids would have been much better off if I had died and my wife had lived.

It seems like a pretty harsh thing to say, and my friend is a very hard-working, good person who has tried his damnedest to be a good father, but he seems very sincere about his opinion. So … the first thing I did was run a cross-tabulation of mother’s education by whether or not the student expected to graduate. I found that students who did not expect to graduate were more than four times as likely to not know their mother’s level of education (17%) as students who did expect to graduate (4%).

That intrigued me enough that I went back to the original data set and pulled out some additional variables, including whether or not there was a mother in the home. When I ran my first analysis with independent variables of student self-rating of school ability (1= far below average) to 7 = (far above average), race (white, black, Hispanic), gender and whether or not there was a mother in the home, I got this lovely ROC curve here.

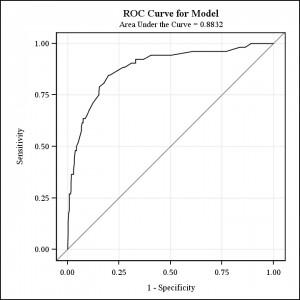Only ability was more important than whether or not there was a mother in the home. Now you could argue there are all sorts of reasons why a mother might not be in the home. Principal among these is that the student may not be living at home but rather with a significant other or spouse. Still, if you got married and moved out of the house, you wouldn’t forget how much education your mother had.

In fact, in another analysis I looked at being married versus single as a predictor and it was significant but not as much as having a mother in the home.

My point (and by now you may have despaired of me ever having one) is that if you just go blithely ahead with mean substitution that you may overlook some very interesting questions that arise in your data, such as why you have missing values in the first place.

I have much more to say about this, but I have a child who wants me to come upstairs and read her Little Women, so it will have to wait.